KALKULUS BAPAK ARI ALDINO APLIKASI TURUNAN PART I

Aplikasi Turunan Part I - Kalkulus

Dari pembahasan mengenai nilai maksimum dan minimum pada tulisan sebelumnya, kita tahu bahwa nilai maksimum (jika ada) suatu fungsi f pada himpunan S adalah nilai f terbesar yang dicapai pada keseluruhan himpunan S. Kadang-kadang diacu sebagai nilai maksimum global, atau nilai maksimum absolut dari f.

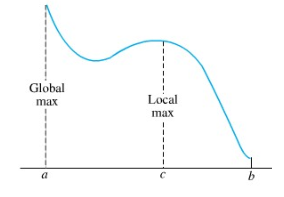
Jadi, untuk fungsi f dengan daerah asal S=[a,b] yang grafiknya diberikan dalam Gambar 1, f(a) adalah nilai maksimum global.

Akan tetapi, bagaimana dengan f(c)? Mungkin saja ia bukan raja dari negara, tetapi paling tidak ia adalah kepala dari lingkungan sekitarnya. Kita sebut f(c) suatu nilai maksimum lokal, atau nilai maksimum relatif. Tentu saja nilai maksimum global otomatis juga nilai maksimum lokal. Gambar 2 melukiskan sejumlah kemungkinan.

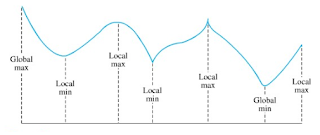
Perhatikan bahwa nilai maksimum global (jika ada) merupakan yang terbesar di antara nilai-nilai maksimum lokal. Demikian pula nilai minimum global adalah yang terkecil di antara nilai-nilai minimum lokal.

Definisi: Maksimum dan Minimum Lokal

Andaikan S, daerah asal f, memuat titik c. Kita katakan bahwa

1.  f(c) nilai maksimum lokal f jika terdapat selang (a,b) yang memuat c sedemikian sehingga       f(c) adalah nilai maksimum f pada (a,b)∩S;
2.  f(c) nilai minimum lokal f jika terdapat selang (a,b) yang memuat c sedemikian sehingga         f(c) adalah nilai minimum f pada (a,b)∩S;
3.  f(c) adalah nilai ekstrim lokal f jika ia berupa nilai maksimum lokal atau minimum lokal. 

Di mana Nilai-nilai Ekstrem Lokal Terjadi?

Teorema Titik Kritis berlaku sebagaimana dinyatakan, dengan ungkapan nilai ekstrim diganti oleh nilai ekstrim lokal, bukti pada dasarnya sama. Jadi, titik-titik kritis (titik ujung, titik stasioner, dan titik singular) adalah calon untuk titik tempat kemungkinan terjadinya ekstrim lokal.

Kita katakan calon karena kita tidak menuntut bahwa setiap titik kritis harus merupakan ekstrim lokal. Bagian kiri grafik dalam Gambar 3 membuat ini jelas. Tetapi, jika turunan adalah positif pada salah satu pihak dari titik kritis dan negatif pada pihak lainnya, maka kita mempunyai ekstrim lokal.

Teorema A: Uji Turunan Pertama

Andaikan f kontinu pada selang terbuka (a,b) yang memuat titik kritis c.

1. Jika f′(x)>0 untuk semua x dalam (a,c) dan f′(x)<0 untuk semua x dalam (c,b), maka                    f(c) adalah nilai maksimum lokalf.
2. Jika f′(x)<0 untuk semua x dalam (a,c) dan f′(x)>0 untuk semua x dalam (c,b), maka                  f(c) adalah nilai minimum lokal f.
3. Jika f′(x) bertanda sama pada kedua pihak c, maka f(c) bukan nilai ekstrim lokal f.

Contoh 1 :

Cari nilai ekstrim lokal dari fungsi f(x)=x2−6x+5, pada (−∞,∞).

Penyelesaian :

Fungsi polinom f kontinu di mana-mana, dan turunannya, f′(x)=2x−6, ada untuk semua x. Jadi, satu-satunya titik kritis untuk f adalah penyelesaian tunggal dari f′(x)=0, yakni x=3.

Karena f′(x)=2(x−3)<0 untuk x<3, f turun pada (−∞,3]; dan karena 2(x–3)>0 untuk x>3, f naik pada [3,∞). Karenaitu,menurut Uji Turunan Pertama, f(3)=−4 adalah nilai minimum lokal f. Karena 3 adalah satu-satunya bilangan kritis, tidak terdapat nilai ekstrim lain. Grafik f diperlihatkan dalam Gambar 4. Perhatikan bahwa dalam kasus ini f(3) sebenarnya adalah nilai minimum (global).

Contoh 3:

Cari nilai ekstrim lokal dari f(x)=(sinx)2/3 pada (−π/6,2π/3).

Penyelesaian:

Titik 0 dan π/2 adalah titik-titik kritis karena f′(0) tidak ada dan f′(π/2)=0.

Sekarang f′(x)<0 pada (−π/6,0) dan pada (π/2,2π/3), sedangkan f′(x)>0 pada (0,π/2). Menurut Uji Turunan Pertama kita simpulkan bahwa f(0)=0 adalah nilai minimum lokal dan bahwa f(π/2)=1 adalah nilai maksimum lokal.

Grafik f diperlihatkan pada Gambar 6.

Uji Turunan Kedua

Terdapat uji lain untuk maksimum dan minimum lokal yang kadang-kadang lebih mudah diterapkan daripada Uji Turunan Pertama. Ia menyangkut penghitungan turunan kedua pada titik-titik stasioner. Ia tidak berlaku pada titik singular.

Contoh 4:

Untuk f(x)=x2−6x+5, gunakan Uji Turunan Kedua untuk mengenali ekstrim lokal.

Penyelesaian:

Ini adalah fungsi dari Contoh 1. Perhatikan bahwa

Jadi, f′(3)=0 dan f′′(3)>0. Karena itu, menurut Uji Turunan Kedua, f(3) adalah nilai minimum lokal.