KALKULUS BAPAK ARI ALDINO TURUNAN PART III
Turunan Part III - Kalkulus
Konsep Turunan
Kesimpulan
Contoh
Notasi Turun dan Rumus Dasar Turunan
Turunan dari sebuah fungsi f dengan variabel x atau f(x) adalah fungsi lain yang dinotasikan dengan f 1(x). jika kita menuliskan y = f(x), adalah koefisensi turunan (difrensial) untuk fungsi f(x). atau turunan dari fungsi f dapat juga dinytakan dengan menggunakan operator D dengan menuliskan D[f(x)]= f 1(x), dapat di tuliskan notasi turunan sebagai berikut.
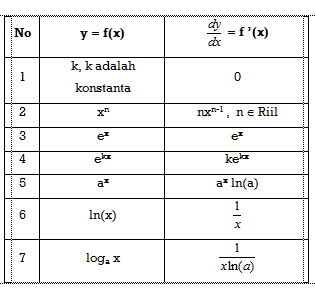
Jika n bilangan rasional , a dan c konstanta sedangkan f"(x) turunan dari f(x) maka berlaku rumus turunan
Fungsi Sifat Turunan
Turunan dari fungsi f adalah fungsi lain f ‘(baca: f aksen), nilai yang untuk setiap nomor c adalah
f ‘(c) = lim \ sb {h \ hingga 0} \ frac {f (c + h) -f (c)} {h}
Meskipun ada batasnya
Contoh 1:
Misalkan f (x) = 13x – 6. Cari f ‘(4).
f ‘(4) = lim \ sb {h \ to 0} \ frac {f (4 + h) -f (4)} {h}
= lim \ sb {h \ hingga 0} \ frac {\ kiri [13 (4 + h) -6 \ kanan] – \ kiri [13 (4) -6 \ kanan]} {h}
= lim \ sb {h \ hingga 0} \ frac {13h} {h}
= lim \ sb {h \ ke 0} 13 = 13
Contoh 2:
f (x) = x3 + 7x, cari f ‘(c)
f ‘(c) = lim \ sb {h \ hingga 0} \ frac {f (c + h) -f (c)} {h}
= lim \ sb {h \ hingga 0} \ frac {\ kiri [(c + h) ^ 3 + 7 (c + h) \ kanan] – \ kiri [c ^ 3 + 7c \ kanan]} {h}
= lim \ sb {h \ hingga 0} \ frac {3c ^ 2j + 3ch ^ 2 + j ^ 3 + 7j} {h}
= lim \ sb {h \ hingga 0} 3c2 + 3ch + h2 + 7
= 3c2 + 7
Contoh Sifat Turunan
Contoh A
Turunan dari fungsi f sehubungan dengan x, ditulis dengan notasi f ‘(x) dengan rumus:
Selain f ‘(x), fungsi anak sering ditulis dengan y,’ dan contoh: Tentukan instance pertama:
f (x) = 2
f (x) = 2x
f (x) = 3×2 +1
f (x) =
Bicara:Perhatikan pembahasan contoh masalah di atas. Dari contoh di atas, kita dapat menyimpulkan bahwa: lebih lanjut untuk yang berikut, properti warisan berikut:
A. Argumen fungsi turunan dari aljabar Jika k adalah angka konstan, untuk setiap x nyata:
f (x) = 5, lalu f ‘(x) = 0
f (x) = 15, lalu f ‘(x) = 0
f (x) = n, lalu f ‘(x) = 0
Jika n adalah bilangan bulat, itu berlaku
Penjelasan
Pengganti h = 0 sehingga semua istilah yang mengandung h adalah 0.
Jika f dan g adalah fungsi dan k adalah angka konstan, maka itu berlaku
Perhatikan uraian pada No. 2, lalu.
Jika f dan g ada dua fungsi dengan f ‘(x) dan g’ (x), maka ini berlaku
Demikian juga, ini berlaku untuk fungsi yang dikurangi.
Jika nilainya … Diketahui bahwa jika f ‘(6) = 40, maka nilai k adalah … Tentukan turunan pertama dari: f (x) = (x – 2) (2x + 3)
Jika f dan g ada dua fungsi dengan f ‘(x) dan g’ (x), maka ini berlaku
menerapkan beberapa contoh literatur menggunakan u dan v, oleh karena itu juga berlaku:
Jika turunan pertama dari fungsi adalah f ‘(x) dan f’ (1) = 3. Maka nilai a adalah …
Bicara:
Contoh B
Tentukan instance fungsi berikut.
1.F (x) = (2x + 3) 5
F (x) = (3×2 – 2) 4
3.F (x) = (x3 + 2x) 5
Jawabannya adalah:
1.F (x) = (2x + 3) 5
Misalnya, u = 2x + 3, oleh karena itu du / dx = u ‘= 2
Y = f (x) = u5 Jadi dy / du = 5u4
F ‘(x) = dy / du. du / dx
= 5u4. 2
= 10u4
= 10 (2x + 3) 4
F (x) = (3×2 – 2) 4
Sebagai contoh, u = 3×2 – 4, oleh karena itu du / dx = u ‘= 6x
Y = f (x) = u4 Jadi dy / du = 4u3
F ‘(x) = dy / du. du / dx
= 4u3. 6x
= 24xu3
= 24 (3×2–4) 3
3.F (x) = (x3 + 2x) 5
Sebagai contoh, u = x3 + 2x, oleh karena itu du / dx = u ‘= 3×2 + 2
Y = f (x) = u5 Jadi dy / du = 5u4
F ‘(x) = dy / du. du / dx
= 5u4. (3×2 + 2)
= 5 (x3 + 2x) 4. (3×2 + 2)
1.f (x) = x3 + x2
2.f (x) = 4×2 + 5x
3.f (x) = 3×5 + 4×3 – 7×2
4.f (x) = 2×4 + 8×3 – x2-9x + 1
5.f (x) = x7 + 2×5 – 6×4 – 9×2 + 11x
Menjawab:
1.f ‘(x) = 3×3-1 + 2×2-1
= 3×2 + 2x
2.f ‘(x) = 4.2×2-1 + 5×1-1
= 8x + 5
f ‘(x) = 3.5×5-1 + 4.3×3-1– 7.2×2-1
= 15×4 + 12×2 – 14x
f ‘(x) = 2.4×4-1 + 8.3×3-1– 2×2-1 – 9
= 8×3 + 24×2 – 2x – 9
f ‘(x) = 7.×7-1 + 2.5×5-1– 6.4×4-1 – 9.2×2-1 + 11×1-1
= 7×6 + 10×4 – 24×3–18x + 11
Contoh di atas adalah fungsi yang berasal dari suku aljabar yang ada.
Baik, sebagai turunan dari operasi dua fungsi aljabar (f (x) dan g (x)). Misalnya, operasi perkalian dan pembagian. Mengapa hanya penggandaan dan pembagian?
Perlu dicatat bahwa operasi penambahan dan pengurangan pada dasarnya mirip dengan operasi yang dijelaskan di atas.
Mari kita lihat lagi fungsi operasi aljabar berikutnya.
F (x) = (x + 2) (2×3 – 5)
F (x) = (x2 + 5) (4×3 – 3x)
3.F (x) = (x + 2) / (3x – 4)
F (x) = (x2 + 1) / (x2 – 1)
Menjawab:
F (x) = (x + 2) (2×3 – 5)
Misalnya, u = x + 2, maka u ‘= 1
dan v = 2×3-5, lalu v ‘= 6×2
f ‘(x) = u’v + uv ’
= 1 (2×3-5) + (x + 2). 6×2
= 2×3-5 + 6×3 + 12×2
= 8×3 + 12×2 – 5
F (x) = (x2 + 5) (4×3 – 3x)
Misalnya, u = x2 + 5, lalu u ‘= 2x
dan v = 4×3-3x, lalu v ‘= 12×2-3
f ‘(x) = u’v + uv ’
= 2x. (4×3-3x) + (x2 + 5). (12×2-3)
= (8×4–6×2) + (12×4–3×2–15)
= 20×4– 9×2-15
3.F (x) = (x + 2) / (3x – 4)
Misalnya, u = x + 5, maka u ‘= 1
dan v = 3x – 4, lalu v ‘= 3
F (x) = (x2 + 1) / (x2 – 1)
Misalnya, u = x2 + 1, lalu u ‘= 2x
dan v = x2 – 1, lalu v ‘= 2x


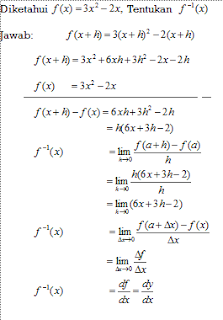







Komentar
Posting Komentar